ஊசல் (இயற்பியல்)

வேறு பயன்பாடுகளுக்கு ஊசல் பக்கத்தைப் பார்க்க.

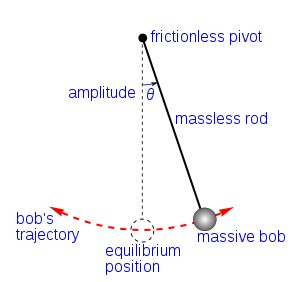தனி ஊசல் - இதில் உராய்வோ வளித்தடையோ கிடையாது

தனி ஊசலின் நேர்போக்குச் சீரிசை இயக்கத்தில் திசைவேகத்தையும் முடுக்கத்தையும் காட்டும் இயங்குப்படம்

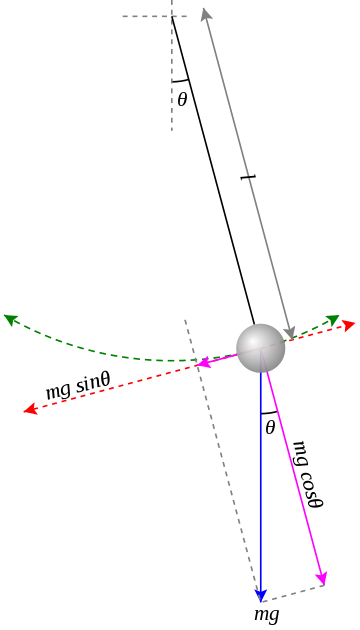ஊசலின் விசையியல் விளக்கப்படம்

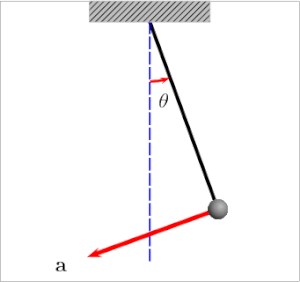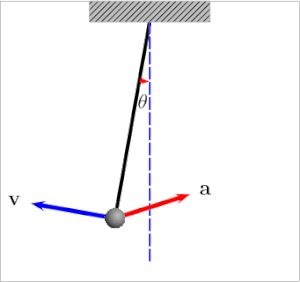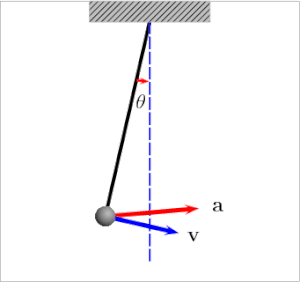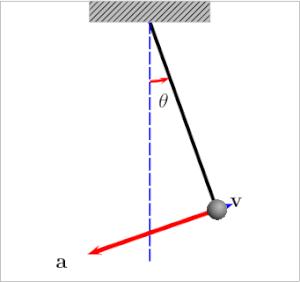
தனி ஊசல், எளிய ஊசல் (simple pendulum) அல்லது பொதுவாக ஊசல் (pendulum) எனப்படுவது புறக்கணிக்கத்தக்க நிறை மற்றும் மீட்சித்தன்மையற்ற நூல் ஒன்றின் ஒருமுனை கட்டப்பட்டும் மறுமுனையில் ஒரு கோளவடிவக் குண்டு (bob) தொங்கவிடப்பட்டும் உள்ள ஓர் அமைப்பு ஆகும். ஊசல் குண்டானது சிறிதளவு இடம்பெயரச் செய்யுமாறு இழுத்துவிடப்பட்டால், அது மையநிலையைப் பொருத்து அலைவுறும். இதற்குக் காரணம் அக்குண்டினை மையநிலையிலிருந்து இடம்பெயரச் செய்யும்போது, அக்குண்டு மையநிலையை நோக்கி அதனை முடுக்குகிற ஒரு மீட்டல் விசைக்கு உள்ளாவதே ஆகும். பின் விட்டவுடன் இம்மீட்டல் விசையோடு குண்டினது நிறையும் சேர்ந்து அவ்வூசலை முன்னும் பின்னுமாய் அலைவுறச் செய்கிறது. ஒரு முழு அலைவை நிறைவு செய்வதற்கு ஊசலானது எடுத்துக் கொள்ளக்கூடிய கால அளவே அலைவுக்காலம்(period) ஆகும். ஊசலின் இடம்பெயர்ந்த நிலையைப் படத்தில் காணலாம்.

1602 ஆம் ஆண்டில் கலீலியோ கலிலி என்பாரால் முதன்முதலில் இது வடிவமைக்கப்பட்டது. அன்று முதல் இது கால அளவீடு செய்யப் பயன்பட்டு வந்தது. இதுவே காலத்தை அளவீடு செய்யக்கூடிய உலகின் மிகத் துல்லியமன தொழில்நுட்பமாக 1930கள் வரை விளங்கியது. இது ஊசல் கடிகாரங்களிலும் முடுக்கமானி, நிலநடுக்கமானி போன்ற கருவிகளிலும் பயன்படுகின்றது.

ஊசலுக்கு நாம் பயன்படுத்தும் 'pendulum' என்கிற சொல் இலத்தின் மொழியின் pendulus என்ற சொல்லிலிருந்து எடுக்கப்பட்டதாகும். இதன் பொருள் 'தொங்கக்கூடிய' என்பதாகும்.

ஊசலின் விசையியல் விளக்கம்

கட்டப்பட்டுள்ள குண்டினுடைய நிறை [math]\displaystyle{ m }[/math] என்றும், ஊசலின் நீளம் [math]\displaystyle{ l }[/math] எனவும் எடுத்துக்கொள்வோம். செங்குத்தான நிலையிலிருந்து நூல் ஏற்படுத்தக்கூடிய கோணம் [math]\displaystyle{ \theta }[/math] எனக் கருதுவோம். நடுநிலையிலிருந்து ஊசல் குண்டானது ஒரு தொலைவிற்குச் செல்கிறது. நடுநிலைக்கும் ஒரு தொலைவிற்கும் இடைப்பட்ட தூரம் [math]\displaystyle{ x }[/math] எனக் கருதலாம். இதுவே அலையின் வீச்சாகும். அத்தொலைவில் குண்டின் எடையானது செங்குத்தாகக் கீழ்நோக்கிச் செயல்படுகிறது. இதன் அளவு [math]\displaystyle{ m g }[/math] என எடுத்துக்கொள்ளப்படுகிறது. ( [math]\displaystyle{ m }[/math] என்பது குண்டினுடைய நிறை, [math]\displaystyle{ g }[/math] என்பது புவியீர்ப்பு முடுக்கம்).

[math]\displaystyle{ m g }[/math] என்கிற இவ்விசையை(எடையை) இரு கூறுகளாகப் பகுக்கலாம்.

1. [math]\displaystyle{ m g cos \theta }[/math] என்கிற கூறு, நூலின் வழியே கட்டப்பட்டுள்ள நிலைப்புள்ளியை நோக்கிச் செயல்படும் இழு விசையைச் சமன் செய்கிறது.
2. [math]\displaystyle{ m g sin \theta }[/math] என்கிற கூறு, நூலுக்குச் செங்குத்தாகச் செயல்படுகிறது. இது சமன் செய்யப்படுவதில்லை. இவ்விசையானது குண்டை மையநிலைகுக் கொண்டு வர முயல்கிறது.

அலையின் வீச்சு சிறியதாக இருப்பதால் ஊசல் குண்டின் பாதை நேர்க்கோடாகக் கருதப்படுகிறது.

கோண இடப்பெயர்ச்சி சிறியதாதலால் ,

[math]\displaystyle{ sin \theta \approx \theta }[/math]

என்று எடுத்துக்கொள்ளப்படுகிறது.

எனவே,

[math]\displaystyle{ F = -{m g \theta} }[/math]

ஆனால்,

[math]\displaystyle{ \theta = \frac{x}{l} }[/math]

எனவே,

[math]\displaystyle{ F = -m g \frac{x}{l} }[/math].

இச்சமன்பாட்டினை நியூட்டனின் இரண்டாம் விதியான ,

[math]\displaystyle{ F = {m a } }[/math]

உடன் ஒப்பிடும்போது,

முடுக்கம், [math]\displaystyle{ a = -\frac{gx}{l} }[/math]

என்பது பெறப்படுகிறது.

இடப்பெயர்ச்சிக்கு எதிர்த்திசையில் முடுக்கம் இருப்பதை எதிர்க்குறி உணர்த்துகிறது.

தனி ஊசலின் இயக்கம் ஒரு தனிச் சீரிசை இயக்கம் என்பதனை இதன் மூலம் அறியமுடிகிறது.

இத்தனிச் சீரிசை இயக்கத்தின் கோண அதிர்வெண்(angular frequency) ω என்று எடுத்துக் கொள்ளப்படுமாயின் ,

தனிச் சீரிசை இயக்கத்தின் முடுக்கத்தை, [math]\displaystyle{ a = -{\omega^2 x } }[/math]

என்று சொல்லலாம்.

இதற்கு முன்னுள்ள சமன்பாட்டின் மூலம் , [math]\displaystyle{ \omega^2 = \frac{g}{l} }[/math]

அல்லது

[math]\displaystyle{ \omega = \sqrt\frac{g}{l} }[/math]

என்கிற சமன்பாட்டை எட்டலாம்.

பொதுவாகவே ஒரு தனிச் சீரிசை இயக்கத்தின் அலைவுக்காலம்,

[math]\displaystyle{ T = {{2 \pi} \over \omega} }[/math].

ஆக, ஊசலின் அலைவுக்காலம், [math]\displaystyle{ T = 2\pi \sqrt\frac{l}{g} }[/math].

எனவே அதிர்வெண், [math]\displaystyle{ n = \frac{1}{2\pi}\sqrt\frac{g}{l} }[/math]

அலைவுக்காலத்தின் திருத்தப்பட்ட சமன்பாடு

ஊசலின் வீச்சைப் பொருத்து அலைவுக்காலம் மாறுபடுவதை இவ்வியங்குப் படம் உணர்த்துகிறது

வீச்சு சிறியதாக இருக்கும்போது அலைவுக்காலம் வீச்சைப் பொருத்து மாறுபடாமல் இருக்கும் பண்பே ஊசலின் மிகப்பெரிய சாதகமாகும். இக்காரணத்திற்காகவே கால அளவீடு செய்வதில் ஊசல் மிகவும் பயன்படுகிறது.

முன்பு தரப்பட்டிருந்த சமன்பாட்டின்படி அலைவுக்காலமானது ஊசலின் நீளத்தையும் [math]\displaystyle{ l }[/math] புவியீர்ப்பு முடுக்கத்தின் அளவையும் [math]\displaystyle{ g }[/math] மட்டுமே சார்ந்திருப்பதாகக் கூறப்பட்டது. ஆனால் வீச்சின் அளவு [math]\displaystyle{ x }[/math] ஒரு குறிப்பிட்ட அளவிற்குக் குறைவாக இருக்கும் வரை மட்டுமே இது உண்மை. வீச்சுக் கோணம் [math]\displaystyle{ \theta_0 }[/math] என்று கொள்ளப்பட்டால்,

[math]\displaystyle{ \T \approx 2\pi \sqrt\frac{l}{g} \qquad \qquad \qquad \theta_0 \ll 1 }[/math]

குறிப்பிட்ட அளவிற்கு மேல், ஊசலின் வீச்சைப் பொருத்துப் படிப்படியாக அலைவுக்காலமும் நேர்த்தகவில் மாறுபடுகிறது. வீச்சுக் கோணம் 180^oயை நோக்கி நகரும்போது அலைவுக்காலமும் முடிவிலியை நோக்கி அணிகுகோடாக(asymptotically) நகர்கிறது. இப்பொழுது அலைவுக்காலத்தின் அளவானது, மேலே உள்ள சமன்பாட்டின் மூலம் கிட்டும் அலைவுக்காலத்தின் அளவை விட அதிகமாக உள்ளது. எனவே மேலே உள்ள சமன்பாட்டில் சில திருத்தங்களைச் செய்வதன் மூலம் அலைவுக்காலத்தின் துல்லியமான மதிப்பைப் பெறலாம். ஊசல் அலைவுக்காலத்தின் திருத்தப்பட்ட சமன்பாட்டைப் பல விதங்களில் வெளிப்படுத்தலாம். அவற்றுள் ஒன்று கீழே உள்ள முற்றிலாத் தொடராகும்.

[math]\displaystyle{ \begin{alignat}{2} T & = 2\pi \sqrt{L\over g} \left( 1+ \frac{1}{16}\theta_0^2 + \frac{11}{3072}\theta_0^4 + \cdots \right) \end{alignat} }[/math]

ஊசல் விதிகள்

தனி ஊசலின் அலைவுகளின் அலைவுக்காலச் சமன்பாட்டிலிருந்து ஊசலின் நான்கு விதிகள் பெறப்படுகின்றன. அவை :

1. நீளத்தின் விதி
2. முடுக்கத்தின் விதி
3. நிறையின் விதி
4. வீச்சின் விதி

நீளத்தின் விதி

தனி ஊசலின் அலைவுகளின் அலைவுக்காலம் [math]\displaystyle{ T }[/math] , ஊசலின் நீளத்தின் [math]\displaystyle{ l }[/math] (length) இருமடி மூலத்திற்கு நேர்த்தகவில் இருக்கும்.

அதாவது, [math]\displaystyle{ T \propto \sqrt{l} \, }[/math]

முடுக்கத்தின் விதி

தனி ஊசலின் அலைவுகளின் அலைவுக்காலம் [math]\displaystyle{ T }[/math] , புவியீர்ப்பின் முடுக்கத்தின் [math]\displaystyle{ g }[/math] (acceleration due to gravity) இருமடி மூலத்திற்கு எதிர்த்தகவில் இருக்கும்.

அதாவது, [math]\displaystyle{ T \propto \frac{1}\sqrt{g} }[/math]

நிறையின் விதி

தனி ஊசலின் அலைவுகளின் அலைவுக்காலம் [math]\displaystyle{ T }[/math] , ஊசல் குண்டின் நிறையையும்(mass) பொருளையும்(material) சார்ந்ததல்ல.

வீச்சின் விதி

சிறிய வீச்சுடன் அலைவுறும் தனி ஊசலின் அலைவுக்காலம் [math]\displaystyle{ T }[/math] , வீச்சினைச்(amplitude) சார்ந்ததல்ல. ஆனால் வீச்சின் அளவு ஒரு குறிப்பிட்ட அளவை விட அதிகமாக இருப்பின், வீச்சைப் பொருத்து ஊசலின் அலைவுக்காலம் மாறுபடும்.

வெளியிணைப்பு

ஊசலின் இயக்கத்தையும் தன்மையையும் இந்த ஒப்பியக்கத்தின் செய்முறைச்சாலையில் செய்து பார்ப்பதுபோல் செய்து பழகி அறியலாம். செய்முறையைத் தொடக்க தொங்கும் குண்டை சுட்டியால் தொடுக்கி இழுத்து நகர்த்தவும்